The h-index in monetised academia

Academics live and die by their h-indices, which contributes to promotions, grant applications and professional reputation.
The key real-world value producing this derived metric is the citation count, which is highly sensitive to which journal you publish into. For example, equivalent articles in PloS One (free) and Nature (pay wall for both author and audience) would be expected receive vastly different citation counts.
Therefore the h-index is significantly dependent on whether you publish for free or via paywall, not just the scientific content of the paper.

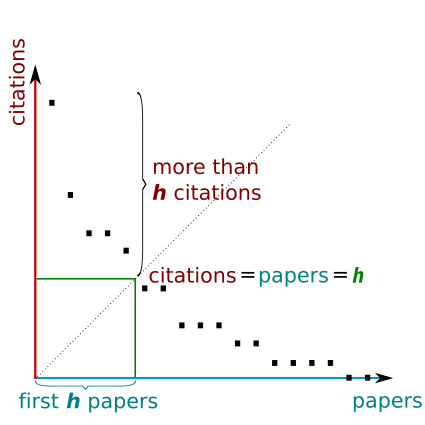
h-index definition (from Wikipedia)

• The definition of the index is that a scholar with an index of h has published h papers each of which has been cited in other papers at least h times.
• This metric would be fine if it weren't true that citation count is confounded by publication destination.
• We could of course do something like plotting # citations vs impact factor of citing article. But this gives no value to the number of articles published by the proband (academic age)

Proposed impactdex

We introduce a "trickle down" effect of impact into the author's "impactdex", or modified h-index

Two different methods come immediately to mind

1. Distort the graph by a factor proportional to r=(impact factor of citing paper)/(impact factor of proband's paper), to shove points toward the f(i)=i diagonal (allowing bigger h)
2. Define the index by a maximal cube with third dimension being r=(impact factor of citing paper)/(impact factor of proband's paper)

The second approach is clearly more aesthetically pleasing, however the implicit meaning of the method is that all three variables (papers, citations, impact of citing work) are independent, while our motivation arises from the observation that this is false.

Method 1

We want to penalise (away from the diagonal) points with r<1, and reward points with r>1.

The ideal 

Define the impactdex such that:

• Map each point (i, f(i)) with gradient f(i)/i, to a point translated point based on r
• Gradient m from origin to translated point:
• If f(i)/i >1: m = f(i)/i-(1-1/r)*(f(i)/i-1) = 1+1/r*(f(i)/i)
• If f(i)/i <1: m = 1-1/r*(f(i)/i)
• Then our corrected index is given by the point whose distance is √[f(i)^2+i^2] from the origin at a gradient of m
• Translated point = (√[f(i)^2+i^2] cos (arctan(m)) , √[f(i)^2+i^2] sin (arctan(m))
• Then the definition of the index is that a scholar with a corrected index of i has published i "corrected papers"
• I.e. it is the h-index of the "corrected scholar"

Method 2

Define the impactdex such that:

• The definition of the index is that a scholar with an index of i has published i papers each of which has been cited in other papers at least i times with a calculated r of at least i
• Where r=(impact factor of citing paper)/(impact factor of proband's paper)
• We seek the maximal cube where one face fills in the h-index criteria like before and the other face fills in the derived r (axis representing David vs. Goliath)

Pitfalls

• Clunky definition, especially method 1
• Increased computation time
• Harder for Google Scholar etc to calculate it, when all it stores natively is citation count (not sure if it has impact factors now)
• People who publish in Nature etc can only do worse with this approach
• Axes in method 2 are not independent

Comments?

What do you think? I'm particularly looking for:

• Someone who could calculate these on a few interesting authors and compare to their h index
• If there's an error in the above, please let me know!